用 python 进行简单滤波器设计

信号分析

首先我们对这个信号进行 fft，观察它的频率成分，代码为：

# -*- coding: utf-8 -*-
import scipy.signal as signal
import numpy as np
import matplotlib.pyplot as plt

'''首先分析信号的频谱'''

fs = 20  # 采样频率
ts = 1 / fs  # 采样间隔
Ts = 4  # 采样总时间
N = int(Ts / ts)  # 采样点数

t = np.linspace(0, Ts, N)  # 采样的横坐标
ft = np.sin(2 * np.pi * t) + (1 / 3) * np.sin(6 * np.pi * t)  # 采样的函数值

# 下面对信号进行 fft
freqx = np.fft.fftfreq(N, d=1 / fs)
fft_vals = np.fft.fft(ft)
fft_theo = 2.0 * np.abs(fft_vals / N)

# 画出采样信号图像
plt.figure(1)
plt.subplot(211)
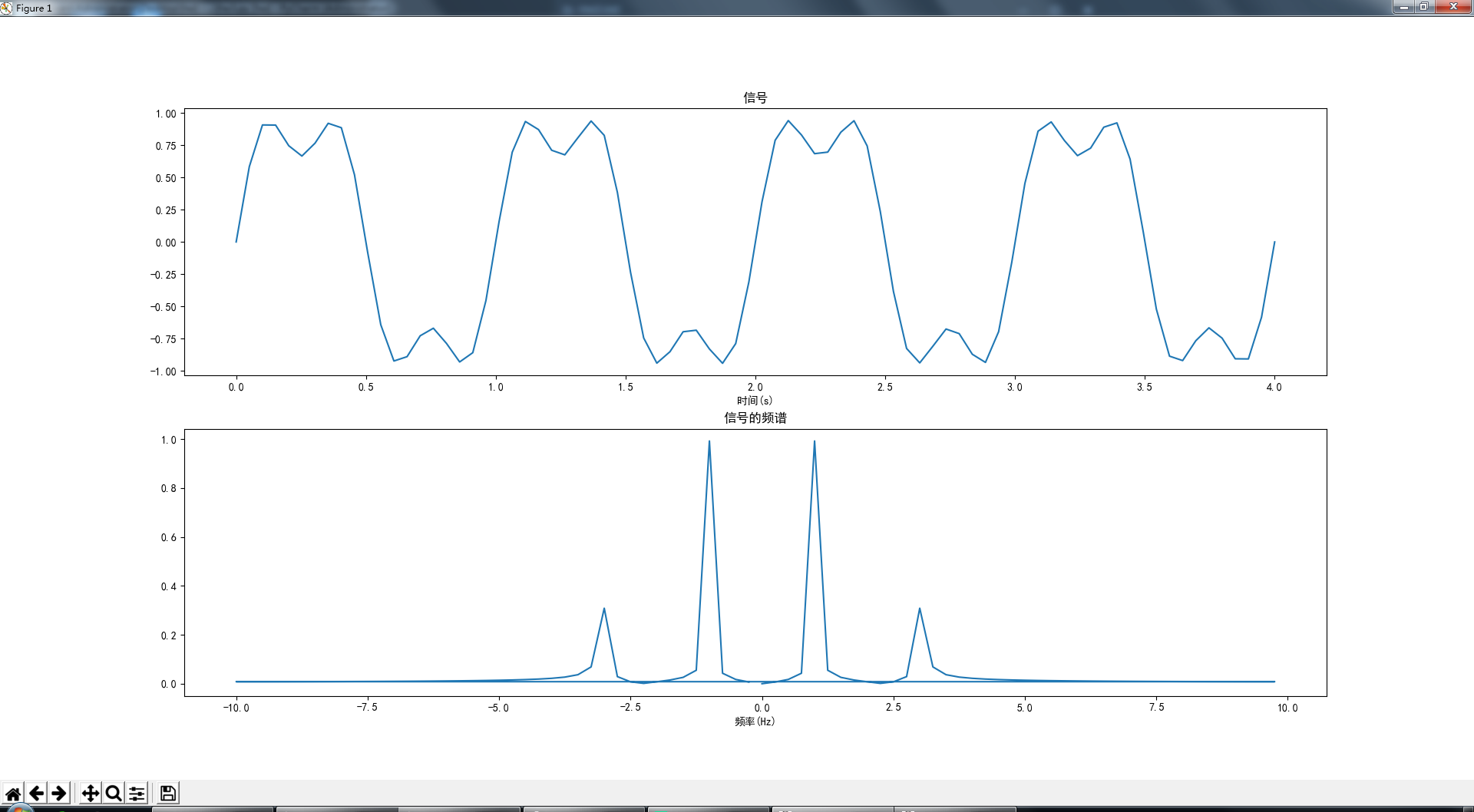
plt.plot(t, ft)
plt.title(u'信号')
plt.xlabel(u'时间(s)')

# 画出采样信号的频谱图
plt.subplot(212)
plt.plot(freqx, fft_theo)
plt.title(u'信号的频谱')
plt.xlabel(u'频率(Hz)')

滤波器设计

我们可以发现，这个信号的有两个频率成分，1 Hz 和 3 Hz，我们需要设计一个低通滤波器，将 3 Hz 的成分去掉，于是我们可以令通带边缘频率为 1.5 Hz，阻带起始频率为 2.5 Hz，通常为了计算方便，利用采样频率将频率值归一化，即将它们除以采样频率，参数计算如下：

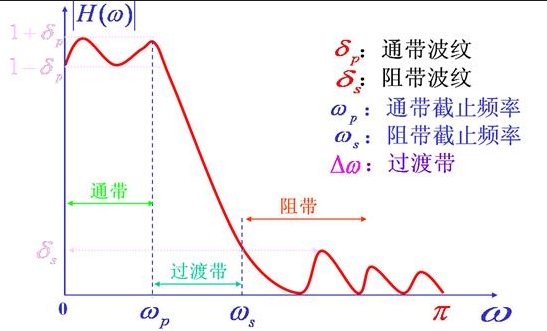
采样频率 $f_s = 20Hz$
通带边缘频率 $f_p = \frac{1.5Hz}{f_s}=0.075Hz$
通带边缘频率 $f_p = \frac{2.5Hz}{f_s}=0.125Hz$
通带边缘角频率 $w_p =2 \pi*f_p=0.15\pi \ [rad/s]$
通带波纹 $\delta_p=0.1$
阻带起始角频率 $w_s= 2\pi * f_s = 0.25 \pi \ [rad/s]$
阻带波纹 $\delta_s=0.01$
截止角频率 $ w_c = \frac{\omega_{p}+\omega_{s}}{2}=0.2 \pi$

下面计算阻带衰减：

$\mathrm{A}_{\mathrm{s}}=-20 \log _{10} \frac{\delta_{\mathrm{s}}}{1+\delta_{\mathrm{p}}}=40.828[db]$

最后可以选用汉明窗，计算窗长：

$\Delta \omega=\omega_{s}-\omega_{p}=0.1 \pi \\ 窗长不小于 \ \mathrm{N}=\frac{6.6 \pi}{\Delta \omega}= 66$

理想低通滤波器的时域理想脉冲响应为：

$h_{d}(n)=\frac{1}{2 \pi} \int_{-\omega_{c}}^{\omega_{\epsilon}} 1 \cdot e^{j \omega n} d \omega \\ =\frac{1}{2 \pi} \cdot \frac{1}{j n} \int_{-\omega_{\epsilon}}^{\omega_{c}} e^{j \omega n} d \omega\\ =\frac{1}{n \pi} \cdot \frac{e^{j \omega_{c} n}-e^{-j \omega_{c} n}}{2 j} \\ =\frac{\sin \left(\omega_{c} n\right)}{\pi n} \\ =\frac{\omega_{c}}{\pi} \sin c\left(\frac{\omega_{c}}{\pi} n\right) \quad n \in(-\infty,+\infty)\\$

下面我们将时域的理想脉冲响应加上窗得到滤波器的时域脉冲响应，并画出滤波器的频域响应：

'''开始设计滤波器除去 3 Hz 的成分'''

# 计算理想滤波器的时域脉冲响应的函数
def h_ideal(N_w, wc):
    n = np.arange(-N_w/2, N_w/2, 1)  # N_w 为窗长
    respond = (wc/np.pi) * np.sinc((wc/np.pi) * n)  # 理想时域响应
    return respond

# 加窗得到滤波器的时域响应
wc = 0.2 * np.pi  # 截止频率
N_w = 66  # 窗长取为 66
h_ideal = h_ideal(N_w, wc)  # （不加窗）理想滤波器脉冲响应
h_filter = h_ideal * np.hamming(66)  # 使用 66 个点的汉明窗

# 画出图形
plt.figure(2)
# 画出滤波器的脉冲响应
plt.subplot(311)
n = np.arange(-N_w/2, N_w/2, 1)*ts  # 乘上时间间隔 ts 才是真实的时间坐标值
plt.stem(n, h_filter, '-')
plt.title(u'滤波器的脉冲响应')
plt.xlabel(u'时间(s)')

# 不加窗的频谱
plt.subplot(312)
w1, h1 = signal.freqz(h_ideal)  # frez 函数用于求离散系统频响特性的函数，返回频率值和频率响应值
plt.plot(w1/(2 * np.pi), 20*np.log10(np.abs(h1)))  # 角频率除以 2pi 变回归一化后的频率，20log() 让幅值的单位变为分贝 dB
plt.title(u'不加窗的频率响应')
plt.xlabel(u'归一化(除以采样频率)后的频率(Hz)')
plt.ylabel(u"幅值(dB)")
# 加窗的频谱
plt.subplot(313)
w2, h2 = signal.freqz(h_filter)
plt.plot(w2/(2 * np.pi), 20*np.log10(np.abs(h2)))
plt.title(u'加窗后的频率响应')
plt.xlabel(u'归一化(除以采样频率)后的频率(Hz)')
plt.ylabel(u"幅值(dB)")

plt.show()

用freqz计算频率响应

freqz用于计算数字滤波器的频率响应，它的调用方式如下：

freqz(b, a=1, worN=None, whole=0, plot=None)

其中b和a是滤波器的系数，b 是滤波器的时域响应 h_filter，worN为所计算的频率点数，whole为0表示计算频率的上限为pi，whole为1表示计算频率的上限为2*pi。

它返回一个组元 (w,h) ，其中w为所有计算了响应的频率数组，其值为归一化的角频率，因此通过w/(2*pi)可以计算出对应的正规化频率。h是一个复数数组，它表示滤波器系统在每个对应的频率点的响应。复数的幅值表示滤波器的增益特性，相角表示滤波器的相位特性。

参考：http://bigsec.net/b52/scipydoc/filters.html

一种简单的加窗方式

firwin(N, cutoff, width=None, window='hamming')

其中 N 为滤波器的长度，cutoff 是归一化后的的频率，window 为所使用的窗函数。

得到的结果如下：

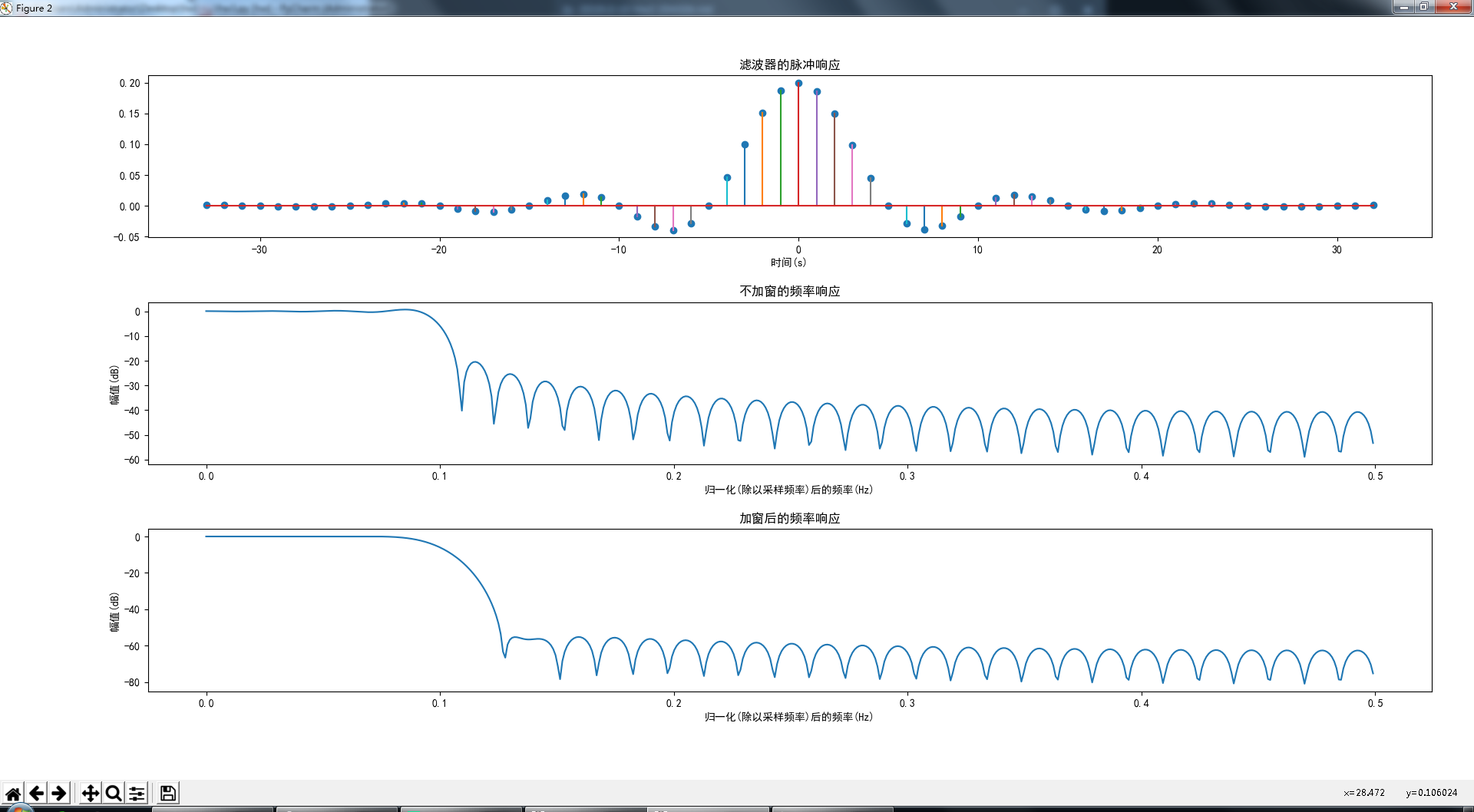
注意此处 $w_c$ 经过了归一化，所以得到的频谱也是经过归一化的频率值，所以过渡带介于 0.075 和 0.125 之间。

进行滤波

上面我们得到滤波器的脉冲响应 h_filter，下面将我们的信号与其做卷积，得到信号通过滤波器的响应：

'''下面将信号与设计的滤波器脉冲响应进行卷积'''

# 将通过滤波器
ft_filtered = signal.lfilter(h_filter, 1, ft)  # 完成滤波过程

# 画出通过滤波器后的信号
plt.figure(3)
plt.subplot(211)
plt.plot(t, ft_filtered)
plt.title(u'经过滤波器的后的信号')
plt.xlabel(u'时间(s)')

# 画出通过滤波器后的信号的频谱
freqx = np.fft.fftfreq(N, d= ts)
fft_vals = np.abs(np.fft.fft(ft_filtered))*2 / N
plt.subplot(212)
plt.stem(freqx, fft_vals, '-')
plt.title(u'经过滤波器后信号的频谱')
plt.xlabel(u'频率(Hz)')

# 调整布局
plt.tight_layout()
plt.subplots_adjust(wspace=0.4, hspace=0.4)
plt.show()

signal.lfilter(b, a, x, axis=-1, zi=None)

此函数可以让信号通过滤波器，实现信号与滤波器脉冲响应的卷积，其中的 b 和 a 是滤波器的系数，x 是输入信号。

由于信号刚进入滤波器进行卷积时会产生延迟，所以得到的结果如下：

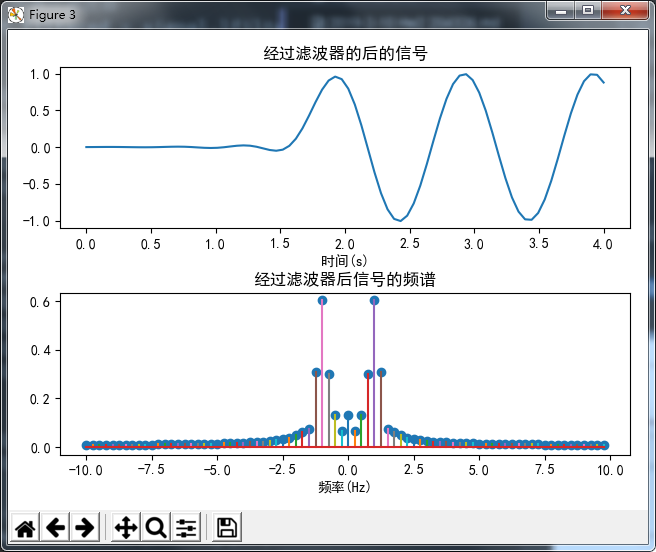
为了得到更准确的频谱，将前 40 个点去掉再做 fft：

# 将通过滤波器
ft_filtered = signal.lfilter(h_filter, 1, ft)
# 取后 40 个点
ft_filtered_clip = ft_filtered[40:]  
t_clip = t[40:]
N_clip = len(t_clip)

# 画出通过滤波器后的信号
plt.figure(3)
plt.subplot(211)
plt.plot(t_clip, ft_filtered_clip)
plt.title(u'经过滤波器的后的信号')
plt.xlabel(u'时间(s)')

# 画出通过滤波器后的信号的频谱
freqx = np.fft.fftfreq(N_clip, d= ts)
fft_vals = np.abs(np.fft.fft(ft_filtered_clip))*2 / N_clip
plt.subplot(212)
plt.stem(freqx, fft_vals, '-')
plt.title(u'经过滤波器后信号的频谱')
plt.xlabel(u'频率(Hz)')

结果为：

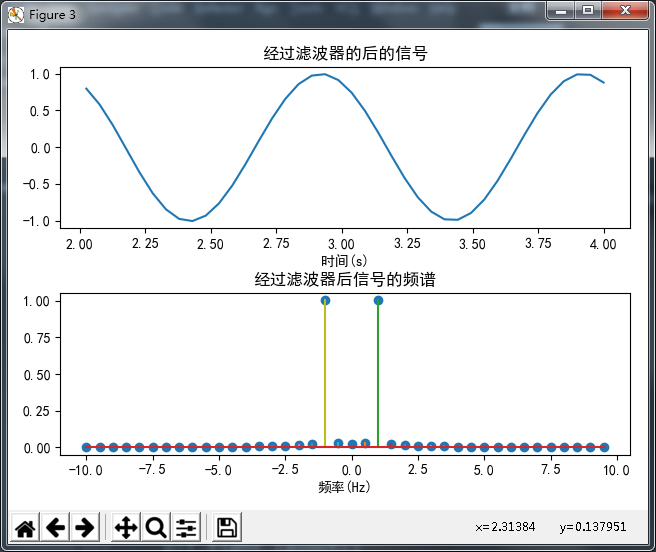
我们可以发现，3 Hz 的成分已经被滤去，只剩 1Hz 的低频部分，滤波成功！

总结

总而言之，设计滤波器的最终目的是获得滤波器系数 b 和 a，在 python 的库 scipy.signal 中有非常多方法可以简单获得 b,a，例如：

1 2	b, a = signal.butter(4, 100, 'low', analog=True) b = signal.remez(length, (0, 0.18, 0.2, 0.50), (0.01, 1))

其中 b 就相当于滤波器的时域脉冲响应 h_fliter.

得到滤波器系数后就可以使用 signal.lfilter(b, a, x, axis=-1, zi=None) 对信号进行滤波了，也可以用 freqz(b, a=1, worN=None, whole=0, plot=None) 作出滤波器的频域响应。

下面是一个例子，更多例子见这个网站。

# -*- coding: utf-8 -*-
import scipy.signal as signal
import numpy as np
import pylab as pl

for length in [11, 31, 51, 101, 201]:
    b = signal.remez(length, (0, 0.18,  0.2,  0.50), (0.01, 1))
    w, h = signal.freqz(b, 1)
    pl.plot(w/2/np.pi, 20*np.log10(np.abs(h)), label=str(length))
pl.legend()
pl.xlabel(u"正规化频率 周期/取样")
pl.ylabel(u"幅值(dB)")
pl.title(u"remez设计高通滤波器 - 滤波器长度和频响的关系")
pl.show()

信号分析

滤波器设计

进行滤波

总结

参考文章